在講麥氏航法之前,必須要先知道麥氏海圖是什麼。
麥氏海圖/麥卡托投影

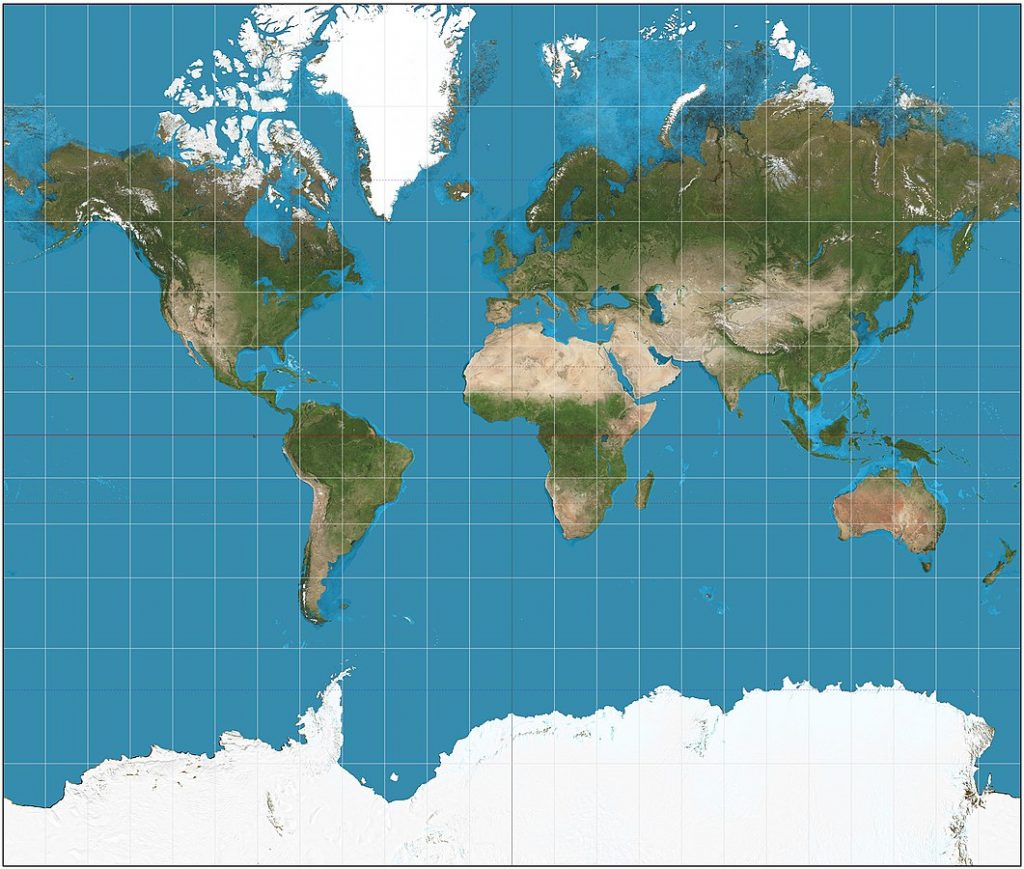
麥氏海圖是用赤道圓筒投影所製作出來的,赤道代表以赤道為切面, 麥氏投影為等角投影1 的一種,代表在地圖上測量的方位為實際方位。但是等角投影的缺點就是越往極點走,面積就越不準確,可以從圖1看到北極和南極的點都從原本的一個點被無限的擴張。
優點
- 角度、方位正確,航行、與測量目標方位時非常方便。
- 角度正確代表形狀正確。
缺點
- 面積不正確,離赤道越遠,面積就會被拉得越大。
- 距離不正確。
Mercator Chart,又稱為麥卡托投影圖(Mercator projection),是一種廣泛使用的地圖投影方法,它以荷蘭地圖製圖師格拉希厄斯·麥卡托(Gerardus Mercator)的名字命名。這種投影法最早出現在16世紀,它使用等角投影方式,即保持角度不變,但是在實現這個目標時,它犧牲了地球表面上的距離和面積的精度。因此,它在海上航行和空中導航中廣泛使用,因為它可以方便地在海圖上測量航線的方向和距離。
在麥氏海圖中,經線是垂直的直線,而緯線是平行於地球赤道的直線。這種投影法最常用於表現高緯度地區的地圖,因為它可以將北極和南極周圍的地區映射成無限大的平面。然而,這種投影方法會導致經線和緯線在遠離赤道的地方會出現明顯的形變,導致較大的扭曲。
雖然麥卡托投影並不是最準確的地圖投影方法,但由於它的廣泛使用和易於理解的特點,它也是最常見的投影方法。
麥氏航法
開船時主要的航線有兩種,一是大圈航線、二就是等角航線。而等角航線的實現主要就是使用麥氏航法2。
優點
相較於大圈航法,麥氏航法比較直觀,海圖上的方位就是實際方位。
使用方法:
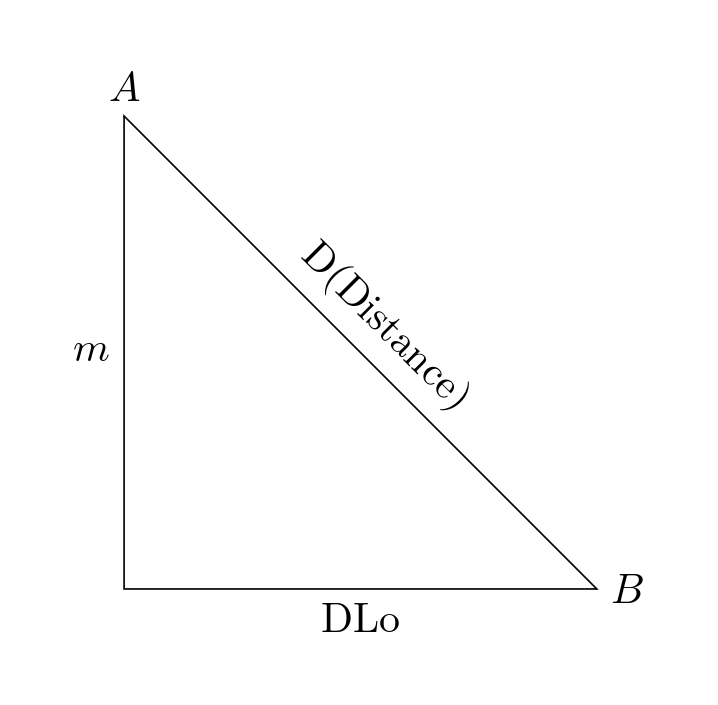
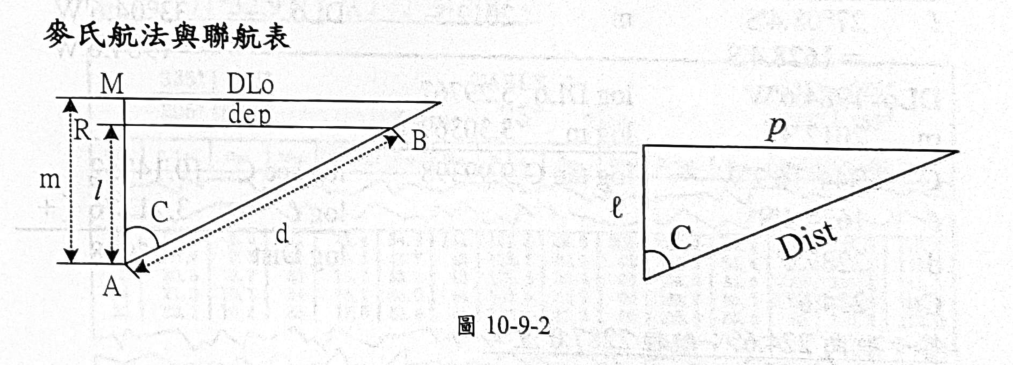
麥氏航法與一般平面航法一樣,都是把球面三角形看成平面直角三角形。重點在於麥氏航法使用的是緯度漸長比數。
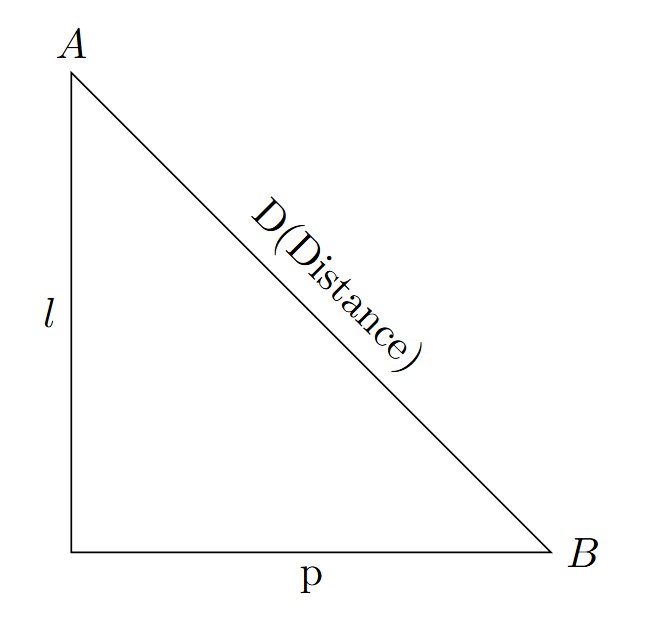
名詞解釋:
m為緯度漸長比數差,D為距離,DLo為經度差。請注意大寫M是緯度漸長比數,小寫m是緯度漸長比數差。
緯度漸長比數(M, Meridional Parts):以赤道一弧分為一單位,沿著子午線從赤道量到該地緯度距離的倍數,即是該地的緯度漸長比數,緯度漸長比數只有數字沒有單位。3
如果有實際畫過麥氏海圖就會懂為什麼要這樣定義。因為經度之間的距離是相等的,所以假設每5度畫一條經線。每兩條經線間的距離在紙上為5公分,則我們就可以知道一度一公分,如果此時查表看到某地緯度緯度漸長比數是120,則我們就可以從赤道開始量2公分就會是該地。但是如果我們把定義從赤道一弧分為一單位改為一海里為一單位的話就會非常複雜了。
緯度漸長比數差(m): 兩地緯度漸長比數的差值。4 假設有A地與B地,A地、B地的緯度漸長比數分別為$$M_A 、M_B$$則 $$m=|M_A – M_B|$$
這個定義在實際上不好使用,實際上在計算時,如果兩地是在同半球則相加、不同半球則相減。5
使用方法講解
例1.某船由甲地(L45°37.0’N,λ69°37.2’W)以麥氏航法(Mercator Sailing)航行至乙地 (L40°28.0’N,λ73°53.7’W),則請問該船之航程距離為何?6
1.先比較兩地經緯度可知,乙在甲的西南方,由此畫一個直角三角形,並將D、DLo、m標上。
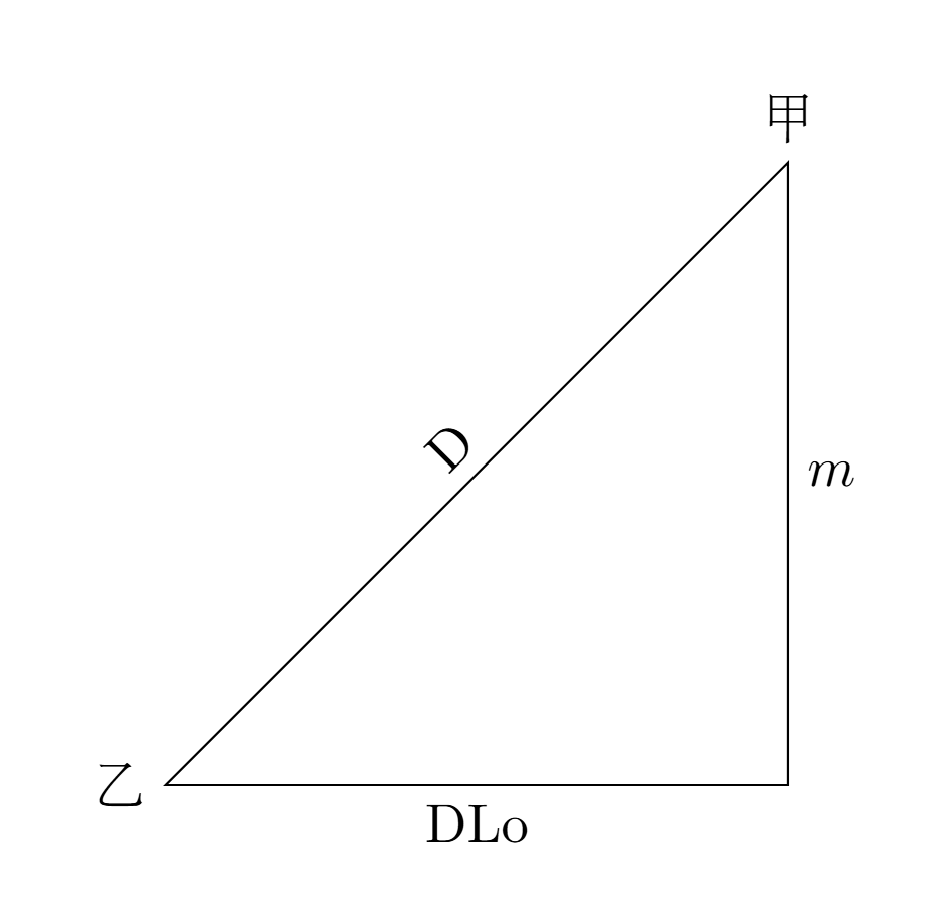
2.再來求DLo、m。
甲、乙兩地的M根據查表得到,M甲=3064.751、M乙=2644.12。
$$DLo = 73°53.7′−69°37.2′=4°16.5′=256.5’$$
$$m=M_甲-M_乙=3064.751-2644.12=420.7$$
3.求航向角Cn
再根據三角形
$$tanCn = m/Dlo$$
$$Cn=tan^-1(Dlo)/m=256.5/420.7=31.3°$$
4.得到航向角後再利用緯度差算出距離D。
兩地緯度差
$$Δφ=45°37.0′−40°28.0′=5°9.0′=309’$$
$$309’/cos31.3°=361.7’$$
答案是361.7海浬
- 高中地理 – 等角投影 [↩]
- 除了麥氏還有平面航法,但麥氏航法的精確度比平面航法高,所以通常使用麥氏航法 [↩]
- American Practical Navigator ’’Bowditch’’ 2019 Volume 1 Number 406 Meridional Parts p.35 [↩]
- American Practical Navigator – Volume I [↩]
- https://encyclopedia2.thefreedictionary.com/meridional+difference [↩]
- 105-4航海學Q.9 [↩]

發佈留言